1. Penjumlahan dan Pengurangan Bentuk Aljabar
Pada
dasarnya, sifat-sifat penjumlahan dan pengurangan yang berlaku pada bilangan
riil, berlaku juga untuk penjumlahan dan pengurangan pada bentuk-bentuk
aljabar, sebagai
berikut.
a. Sifat Komutatif
a + b = b + a, dengan a dan
b bilangan riil
b. Sifat Asosiatif
(a + b) + c = a + (b
+c), dengan a, b, dan c bilangan riil
c. Sifat Distributif
a (b + c)
= ab + ac, dengan a, b, dan c bilangan riil
Contoh Soal 1:
Sederhanakan
bentuk-bentuk aljabar berikut.
a. 6mn
+ 3mn
b. 16x
+ 3 + 3x + 4
c. –x
– y + x – 3
d. 2p
– 3p2 + 2q – 5q2 + 3p
e. 6m
+ 3(m2 – n2) – 2m2 +
3n2
Jawab:
a. 6mn
+ 3mn = 9mn
b. 16x
+ 3 + 3x + 4 = 16x + 3x + 3 + 4
= 19x +
7
c. –x
– y + x – 3 = –x + x – y – 3
= –y – 3
d. 2p
– 3p2 + 2q – 5q2 + 3p = 2p
+ 3p – 3p2 + 2q – 5q2
= 5p
– 3p2 + 2q – 5q2
=
–3p2 + 5p – 5q2 + 2q
e. 6m
+ 3(m2 – n2) – 2m2 +
3n2 = 6m + 3m2 – 3n2
– 2m2 + 3n2
= 6m + 3m2 – 2m2 – 3n2
+ 3n2
= m2 + 6m
Contoh Soal 2:
Tentukan
hasil dari:
a.
penjumlahan 10x2 + 6xy – 12 dan –4x2
– 2xy + 10,
b.
pengurangan 8p2 + 10p + 15 dari 4p2
– 10p – 5.
Jawab:
a. 10x2
+ 6xy – 12 + (–4x2 – 2xy + 10) = 10x2
– 4x2 + 6xy – 2xy – 12 + 10
= 6x2 + 4xy – 2
b. (4p2
– 10p – 5) – (8p2 + 10p + 15) = 4p2
– 8p2 – 10p –10p – 5 – 15
= –4p2 – 20p – 20
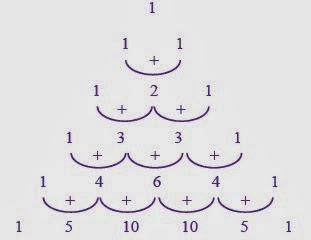
4. Perpangkatan Bentuk Aljabar
Untuk
memudahkan penguraian perpangkatan bentuk-bentuk aljabar tersebut, kamu bisa
menggunakan pola segitiga Pascal . Sekarang, perhatikan pola segitiga Pascal
berikut.
2. Perkalian Bentuk Aljabar
Perhatikan
kembali sifat distributif pada bentuk aljabar. Sifat distributive merupakan
konsep dasar perkalian pada bentuk aljabar. Untuk lebih jelasnya, pelajari
uraian berikut.
a. Perkalian Suku Satu dengan Suku Dua
Contoh Soal:
Gunakan hukum distributif untuk
menyelesaikan perkalian berikut.
a. 2(x + 3) = 2x + 6
b. –5(9 – y)
= –45 + 5y
c. 3x(y +
5) = 3xy + 15x
d. –9p(5p
– 2q) = –45p2 + 18pq
b. Perkalian Suku Dua dengan Suku Dua
Contoh Soal 1:
a. (x
+ 5)(x + 3) = (x + 5)x + (x + 5)3
= x2
+ 5x + 3x + 15
= x2
+ 8x + 15
b. (x
– 4)(x + 1) = (x – 4)x + (x – 4)1
= x2
– 4x + x – 4
= x2
– 3x – 4
c. (2x
+ 4)(3x + 1) = (2x + 4)3x + (2x + 4)1
= 6x2
+ 12x + 2x + 4
= 6x2
+ 14x + 4
d.
(–3x + 2)(x – 5) = (–3x + 2)x + (–3x +
2)(–5)
= –3x2
+ 2x + 15x – 10
= –3x2+ 17x – 10
Contoh Soal 2:
Diketahui
sebuah persegipanjang memiliki panjang (5x + 3) cm dan lebar (6x–
2) cm. Tentukan luas persegipanjang tersebut.
Jawab:
Diketahui : p
= (5x + 3) cm dan l = (6x – 2) cm
Ditanyakan :
luas persegipanjang
Luas = p ×
l
=
(5x + 3)(6x – 2)
= (5x + 3)6x + (5x
+ 3)(–2)
= 30 x2 + 18x
– 10x – 6
= 30 x2 + 8x –
6
Jadi,
luas persegipanjang tersebut adalah (30x2 + 8x – 6) cm2
3. Pembagian Bentuk Aljabar
Tentukan hasil pembagian berikut.
4. Perpangkatan Bentuk Aljabar
Bilangan
berpangkat didefinisikan sebagai berikut.
an = a x a x a x …x a (sebanyak
n faktor)
Untuk a
bilangan riil dan n bilangan asli. Definisi bilangan berpangkat
berlaku juga pada bentuk aljabar. Untuk lebih jelasnya, pelajari uraian
berikut.
a. a5 = a × a × a
× a × a
b. (2a)3 = 2a ×
2a × 2a = (2 × 2 × 2) × (a × a × a) = 8a3
c. (–3p)4 = (–3p)
× (–3p) × (–3p) × (–3p)
= ((–3) × (–3) × (–3) ×
(–3)) × (p × p × p × p)
= 81p4
d. (4x2y)2
= (4x2y) × (4x2y) = (4 × 4) × (x2 × x2)
× (y × y) = 16x4y2
Sekarang,
bagaimana dengan bentuk (a + b)2? Bentuk (a + b)2 merupakan
bentuk lain dari (a + b) (a + b). Jadi, dengan menggunakan sifat
distributif, bentuk (a + b)2 dapat ditulis:
(a
+ b)2 = (a + b) (a + b)
= (a + b)a + (a
+ b)b
= a2 + ab +
ab + b2
= a2
+ 2ab + b2
Dengan
cara yang sama, bentuk (a – b)2 juga dapat ditulis
sebagai:
(a
– b) 2 = (a – b) (a – b)
= (a – b)a + (a –
b)(–b)
= a2 – ab – ab
+ b2
= a2
– 2ab + b2
Contoh Soal:
Tentukan hasil kuadrat dari bentuk aljabar berikut.
a. (x
+ 1)2 = (x) 2 + 2(x)(1) + (1) 2
= x2 + 2x + 1
b. (2p – 3q) 2 = (2p) 2
– 2(2p)(3q) + (3q) 2 = 4p2 –
12pq + 9q2
Selanjutnya, akan diuraikan bentuk (a
+ b)3, sebagai berikut.
(a + b)3 = (a + b) (a + b)2
= (a
+ b) (a2 + 2ab + b2) (a+b)2
= a2 + 2ab + b2
= a3 + 2a2b
+ a2b + ab2 +2ab2
+ b3 (suku yang sejenis dikelompokkan)
= a3 + 3a2b
+ 3ab2 + b3 (operasikan
suku-suku yang sejenis)

Hubungan antara segitiga Pascal dengan perpangkatan suku dua bentuk
aljabar adalah sebagai berikut
Dengan
menggunakan pola segitiga Pascal dan aturan perpangkatan variabel,
bentuk-bentuk perpangkatan suku dua (a + b)3, (a + b)4, (a + b)5,
dan seterusnya dapat diuraikan sebagai berikut.
(a
+ b)3 = a3 + 3a2b + 3ab2
+ b3
(a
+ b)4 = a4 + 4a3b + 6a2b2
+ 4ab3 + b4
(a
+ b)5 = a5 + 5a4b +
10a3b2 + 10a2b3
+ 5ab4 + b5
dan seterusnya.
Perpangkatan bentuk aljabar (a – b)n dengan n bilangan
asli juga mengikuti pola segitiga Pascal. Akan tetapi, tanda setiap
koefisiennya selalu berganti dari (+) ke (–), begitu seterusnya. Pelajarilah
uraian berikut.
(a – b)2 = a2 – 2ab + b2
(a – b)3 = a3 – 3a2b
+ 3ab2 – b3
(a – b)4 = a4 – 4a3b + 6a2b2
– 4ab3 + b4
(a – b)5 =
a5 – 5a4 b + 10a3b2 – 10a2b3
+ 5ab4 – b5
Contoh Soal:
Uraikan perpangkatan bentuk-bentuk aljabar
berikut.
a. (x + 5)2 = x2
+ 2(x)(5) + 52
= x2 + 10x
+ 25
b. (2x + 3)3 = (2x)
3 + 3(2x) 2 (3) + 3(2x)(3) 2 + 33
= 8x3 + 36x2
+ 54x + 27
c. (x – 2)4 = x4 – 4 (x)
3(2) + 6(x) 2 (2) 2 – 4(x)(2) 3
+ 24
= x4 – 8x3
+ 24x2– 32x + 16
d. (3x – 4) 3 = (3x)
3 – 3(3x) 2 (4) + 3(3x)(4) 2 – (4)
3
=
27x3 – 108x2 + 144x – 64
DAFTAR PUSTAKA
Agus,
Nuniek Avianti. 2007. Mudah Belajar Matematika 2: untuk Kelas VIII SMP/MTs. Jakarta: Pusat
Perbukuan, Departemen Pendidikan Nasional


Tidak ada komentar:
Posting Komentar
BERIKAN TANGGAPAN ATAU PERTANYAAN UNTUK TULISAN INI.